MATEMÁTICAS
Semejanza en cuadriláteros
Aprendizaje
esperado: Resuelve problemas de congruencia y semejanza
que implican utilizar estas propiedades en triángulos o en cualquier figura.
Énfasis: Resolver
problemas que impliquen las propiedades de semejanza de cuadriláteros
¿Qué vamos
a aprender?
Trabajarás
con la resolución de problemas de semejanza que implican utilizar estas
propiedades en triángulos o en cualquier figura.
Recuerda
brevemente los conceptos de:
- Semejanza
- Razón
- Proporcionalidad
- Características básicas de los
cuadriláteros, particularmente de los cuadrados y rectángulos.

La
proporción es la igualdad de dos razones. A entre b igual a c entre d.

El cuadrado
y el rectángulo son cuadriláteros con la característica adicional de que todos
sus lados miden 90º.

Después de
esta revisión, comienza con el siguiente el problema 1.
Aida, tiene
en su casa dos televisores de pantalla plana que son de diferente tamaño. En el
cuarto de su abuelita hay un tercer televisor, el cual es de modelo antiguo.

Hace unos
días, mientras Aída veía su clase de matemáticas del programa Aprende en casa
II en el televisor de su abuelita, notó que las imágenes se veían algo
diferentes a las que se ven en sus televisores de pantalla plana. Al terminar
su clase, quiso saber el porqué de la diferencia entre las imágenes de las
pantallas planas y las del televisor de su abuelita.

Aída decide
preguntarle a su papá, y él le responde que es debido a que el televisor de su
abuelita es antiguo. Ella no se conforma con la respuesta, y decide
encontrar otra razón. Observa:
Aída observa los televisores y, después de analizar el problema, toma una cinta métrica y mide el largo y ancho de la zona de la pantalla de cada televisor.
Después de
medir cada uno de los televisores, anota los resultados en su libreta de
matemáticas. Así:

¿Podrías
ayudarla a saber por qué la imagen es diferente? ¿Qué tiene que hacer con las
mediciones para encontrar alguna razón matemática que explique la diferencia?
Lo primero
que considera Aída es que en todos los casos las pantallas son rectángulos, así
que con sus conocimientos de matemáticas decide encontrar la razón, es decir,
la constante numérica que obedece a la relación entre dos cantidades, que en
este caso se puede hacer con la medida del largo y ancho de cada uno de los
televisores. Para ello, divide ambas cantidades en los tres casos, obteniendo
lo siguiente:

Si observas
la tabla, lo que encuentras es que los televisores de pantalla plana guardan la
misma relación numérica entre el largo y el ancho, es decir, existe una
constante a la que le llamaremos “k” o constante de proporcionalidad.
¿Qué puedes
notar de los resultados obtenidos?

De esta
manera puedes saber que los rectángulos de dos de los televisores, las
pantallas planas, tienen lados proporcionales.
También
sabes que, al ser rectángulos todos, los ángulos que los forman tienen 90°, por
lo que en todos ellos podríamos pensar que debería existir una condición de
semejanza en las figuras, sin embargo, como observaste en la tabla, en el tv de
la abuela, la razón “k” no es la misma, por lo que la pantalla es un rectángulo
que no guarda la misma proporción que el de las pantallas planas.

Ahora
puedes entender que la imagen en el televisor de la abuela no se vea igual que
en las pantallas planas, pues la relación de largo y ancho es diferente.
Así, tenemos que, en el caso de las dos pantallas planas, la imagen se percibe de la misma manera, a pesar de la diferencia de tamaño, porque ambas pantallas son rectángulos que tienen ángulos iguales y lados proporcionales. Esto nos lleva a decir que ambas pantallas son semejantes.
Ahora
observa una segunda situación:
Lety trabaja con un impresor, y se encarga de acomodar la materia prima y los trabajos que se realizan.
Un día, acomodando los materiales, observa sobre la mesa de trabajo 3 tarjetas de diferentes tamaños, y cada una con una de sus diagonales trazadas.
Ella decide acomodarlas en su lugar, pero no sabe a qué paquete pertenecen. Para ello aprovecha que en esa mesa hay un tapete de corte con cuadriculado y decide colocarlas alineadas para saber rápidamente su tamaño.
Al hacerlo,
las pone todas juntas un momento y se percata de que si las coloca alineadas
por un vértice pasa lo siguiente:

Dos de las
tarjetas coinciden en sus diagonales, y la otra no.
¿Por qué
sucede esto?
¿Qué
características pueden tener las que coinciden?
Observa la
siguiente imagen.

En la
imagen de la izquierda, la diagonal de la tarjeta rayada y la diagonal de la
tarjeta en blanco no coinciden.
¿Y qué
observas en la imagen de la derecha? ¿Qué es lo que sucede?
Las dos
diagonales de las dos tarjetas coinciden. Apóyate de la situación en que
se forman dos triángulos en cada imagen.
Tienes que,
con la diagonal trazada, puedes observar dos triángulos, el triángulo ABC y el
triángulo ADE, y de ahí tienes lo siguiente:

El ÐABC=ÐADE ,
debido a que las tarjetas son rectangulares y ambos miden 90°.
ÐBAC=ÐDAE, en
ambos triángulos por construcción, es decir, por la coincidencia de la diagonal
de los rectángulos.

Y bajo este
razonamiento:
Ð BCA=Ð DEA ,
debido a que, si ya tienes dos ángulos iguales en dos triángulos, el tercero de
ellos es igual en ambos casos, pues es lo que resta para completar 180° que
es la suma total de los ángulos interiores de cualquier triángulo.
Recuerda
que, en la semejanza de triángulos, si se tienen los tres ángulos iguales en
dos triángulos, ambos son semejantes, lo cual se expresa de la siguiente
manera:
rABC ~ rADE
Ahora observa qué tamaños de tarjetas son cuadriláteros semejantes y a qué tipo de tarjeta pertenecen.
La tarjeta 1 y la tarjeta 3 son figuras semejantes debido a que ambas están formadas de dos triángulos.
La tarjeta
1 es una Ficha de presentación cuyas medidas son 9 x 6 cm, la tarjeta 3 es una
Ficha bibliográfica con las siguientes dimensiones 15 x 10cm. Por último,
la tarjeta 2 que es una Ficha hemerográfica mide 12.5 x 7.5 cm.

Entonces
podemos concluir que las fichas de presentación y la bibliográfica están
construidas de modo que sus rectángulos son semejantes. Así, has resuelto este
problema: apoyándote en la semejanza de triángulos.
Ahora,
Lety sabe a qué paquete corresponde cada una de ellas, y algo más.
Recuerda dos
cuadriláteros son semejantes si hay una correspondencia entre sus vértices de
tal manera que los ángulos correspondientes son iguales y los lados
correspondientes son proporcionales.
¿Qué
hacemos?
Revisa la
siguiente situación:
Samuel, es
aficionado a la astronomía. Utilizando su telescopio y una cámara fotográfica,
obtuvo una magnífica fotografía de la Luna.

Imprimió
varias fotografías de esa imagen en diferentes tamaños. Obsérvalas:

A Samuel
también le gustan las matemáticas, y al observar las fotografías recordó el
tema de semejanza en cuadriláteros. ¿Podrías ayudar a Samuel, a determinar
cuáles de las siguientes fotografías de la Luna son semejantes entre sí?
¿Les ayuda
saber las medidas del ancho y el largo de cada rectángulo? ¿Cómo utilizan estos
datos para saber qué fotografías (como verás todas son rectángulos) son
semejantes?
De acuerdo,
ayudemos a Samuel. Primero calcula la razón de semejanza entre dos
fotografías. Por ejemplo, calculemos el cociente entre lados homólogos o
correspondientes de las fotos A y B, observa:

Al calcular
el cociente entre el largo de la foto A y el de la foto B obtienes la razón
1.44 y al calcular el cociente entre el ancho de la foto A y el de la foto B
obtienes la razón 1.54; lo cual indica que estas dos fotografías no son
semejantes.
Obtén ahora
las razones de los lados correspondiente de las fotografías A y C.
Al realizar
el cociente de los lados correspondientes, obtienes lo siguiente:
Que la
razón del largo de estas dos fotos es igual a 2.88, mientras que la razón del
ancho es de 3.08.
Por lo tanto, estas dos fotografías, tampoco son semejantes.
Que la
razón del largo de estas dos fotos es igual a 2.88, mientras que la razón del
ancho es de 3.08. Por lo tanto, estas dos fotografías, tampoco son semejantes.
Todavía no
has encontrado dos fotografías semejantes, pero falta determinar si las fotos A
y D y si las fotos B y C puedan serlo, continua:
Calcula el
cociente de los lados correspondientes tanto del largo como del ancho entre
ambas fotografías. Así obtienes para el largo la razón 1.2 y para el ancho lo
mismo, es decir 1.2
Puedes
afirmar que al menos las fotografías A y D son fotografías semejantes, pero
¿Serán semejantes las fotografías B y C?
Al comparar
los lados homólogos, notas que ambas razones son la misma, es decir 2, por lo
tanto, los lados de las fotografías son proporcionales y de esta manera sabes
que son semejantes.

No olvides
que para poder afirmar que dos rectángulos son semejantes, es necesario
verificar que se cumpla la proporcionalidad entre las longitudes de sus lados
diferentes, en este caso esa proporcionalidad se representa con la letra “ka”.

Los
rectángulos pueden ser semejantes si cumplen con ser proporcionales en sus
lados. Pero ¿Qué tal si observas semejanza en otros cuadriláteros, como el caso
de los cuadrados?
Observa lo
siguiente:

Hay cuatro
cuadrados, ¿Qué procedimiento utilizarías para saber qué cuadrados son
semejantes?
Recuerda
que los cuadrados tienen lados iguales, así, puedes realizar lo siguiente:
En todos los casos se utilizan letras minúsculas para designar los lados de cada cuadrado.
Todas las
razones son iguales y además siempre son igual a 1.
Entonces,
puedes afirmar que todo cuadrado que existe es proporcional a otro por las
medidas de sus lados.

Entonces:

Dos
cuadrados siempre son semejantes en virtud de que todos sus ángulos miden 90º y
todos sus lados cumplen con la misma razón. K es = a L entre l

¿Y qué tal
con otros cuadriláteros que no sean rectángulos ni cuadrados? ¿Podrías, por
ejemplo, identificar cuáles de los siguientes cuadriláteros son semejantes?
Aquí tienes
4 diferentes cuadriláteros, ¿Tienen la misma forma todos? ¿Y qué dices de sus tamaños?
¿Son todos iguales? obsérvalos cuidadosamente ¿Cuál de ellos es semejante al
cuadrilátero ABCD? ¿Cómo lo resolverías?

Al ampliar
el cuadrilátero ABCD, el resultado será otro cuadrilátero semejante, y solo
cambiarán las longitudes de sus lados, pero no la medida de sus ángulos,
observa cuánto miden los ángulos del cuadrilátero ABCD.
Ahora
compara estas medidas con las del resto de los cuadriláteros.
Las medidas
de los ángulos del cuadrilátero EFGH son 79º, 128º, 63º y 90º
Los ángulos
del cuadrilátero IJKL miden 68º, 139º, 63º y 90º
Por último,
el cuadrilátero MNOP tiene las siguientes medidas de ángulos 62º, 146º, 63º y
desde luego 90º

Compara
primero los cuadriláteros ABCD y EFGH, observa sus ángulos, y verás claramente
que, por ejemplo, el ángulo b no es congruente al ángulo F, y por lo tanto
podemos decir que el cuadrilátero ABCD no es semejante al cuadrilátero EFGH,
pues no tienen la misma forma.

Y qué tal
si comparas ahora al cuadrilátero ABCD con el IJKL. ¿Es el ángulo B congruente
con el J? No, lo que significa que estos dos cuadriláteros tampoco son
semejantes.

Ahora sí,
seguro puedes responder:
- ¿Cuál cuadrilátero es
semejante al cuadrilátero ABCD?
Los ángulos
del cuadrilátero ABCD son congruentes con los del MNOP, además sus lados son
proporcionales, el primer cuadrilátero está ampliado al doble. Obteniendo como
resultado el cuadrilátero MNOP.

Los cuadriláteros ABCD y MNOP son semejantes:
El uso del
concepto de semejanza de cuadriláteros es más útil de lo que te puedes
imaginar.
¿Te
acuerdas de Samuel? Pues bien, después de imprimir sus magníficas fotografías,
buscó en internet y se enteró que existen diferentes medidas de papel para
impresión y encontró la siguiente imagen:
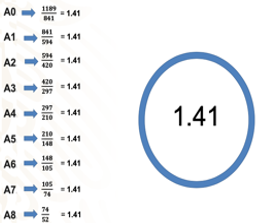
Aquí están
representados los formatos de 8 diferentes tamaños de papel.

Los
formatos en la imagen están superpuestos, y son denominados tamaño A0, A1, A2,
A3, A4, A5, A6, A7 y A8.


Observa a
qué medida corresponde cada formato.

Al terminar
de observar las medidas, Samuel se preguntó: ¿Cuál será la razón entre el lado
mayor y el lado menor de cada uno de los diferentes tamaños de papel? ¿Serán
semejantes? Ayuda a Samuel, una vez más:
Como todas las razones son la misma, las bases y las alturas de los diferentes formatos son proporcionales.

Recuerda:
Dos cuadriláteros son semejantes si tienen la misma forma, pero no
necesariamente el mismo tamaño. Al reducir o ampliar un cuadrilátero, el
resultado es otro cuadrilátero semejante al primero, además sus ángulos son
iguales.
El Reto de
Hoy:
Hoy
trabajaste en la resolución de problemas de congruencia y semejanza que
implican utilizar estas propiedades en triángulos o en cualquier figura.
Un
resultado importante que observaste fue el de que todos los cuadrados son
semejantes. ¿Lo habías pensado?
No olvides
revisar la congruencia y la semejanza en tus libros de tercer grado de
Matemáticas y dar un repaso.
LENGUA MATERNA
Escribir para reescribir
Aprendizaje
esperado: Argumenta sus puntos de vista respecto al tema
que desarrolla en un Ensayo y lo sustenta con información de las fuentes
consultadas.
Énfasis: Integrar
información proveniente de diferentes textos.
¿Qué vamos
a aprender?
Esta sesión
tiene como propósito integrar la información proveniente de diferentes
textos en un ensayo. Este aprendizaje te será muy útil, ya que el ensayo
es una herramienta para poner en orden tus ideas, al momento de querer
compartir nuestra opinión.
Recuerda
que todo lo que aprendas hoy, es para reforzar tu conocimiento, así que te
recomiendo llevar un registro de las dudas, inquietudes o dificultades que
surjan al resolver los planteamientos. Muchas de estas, las podrás resolver al
momento de consultar tu libro de texto y revisar tus apuntes.
Los textos
informativos pueden ser: Informes, artículos o ensayos, es importante elaborar
un borrador, que consiste en una aproximación del texto a construir. En este
primer escrito tienes la oportunidad de plasmar tus ideas previas, y
subsecuentemente, ir incorporando más información para después jerarquizarla, y
decidir si expones datos duros, o es mejor hacer una interpretación de ellos,
entre otros aspectos, que seguramente ya tienes en mente.
Con la
información que cuentas en las fichas de trabajo, harás una primera selección
de esta para determinar qué es lo más conveniente para incluir como parte de la
introducción de tu ensayo, así como cuáles serán las citas textuales o datos
que respalden tus argumentos con respecto al tema. De igual manera podrás ir
distinguiendo cuál será parte de la conclusión.
Un borrador
entonces, es un escrito previo, donde puedes poner y quitar y probar cuál puede
ser la mejor versión de tu ensayo final.
En este primer
documento de “el borrador” es una herramienta muy útil ya que ahí puedes hacer
todos los cambios que se requieran, por lo que puedes: borrar, tachar, poner
marcas que te ayuden a identificar la información que quieras destacar, los
datos de los cuales quieras prescindir, en dónde quieres profundizar, verificar
si la postura ante el tema está desarrollada lo suficiente, y sí es justo lo
que quieres transmitir.
Este primer
documento (borrador) es el esqueleto del documento final al que se deberá ir “nutriendo”
con la información que deseas dar a conocer. Inicia entonces con la redacción
de un ENSAYO.
Durante la
redacción de un Texto Informativo, es fundamental organizar las ideas que vas a
exponer, de tal forma que estas tengan sentido y puedan ser comprendidas de
manera clara por tus lectores. Por lo tanto, es ideal que al escribir el texto
se haga de acuerdo con una estructura, organización y desarrollo claro y
preciso de las ideas, descripciones y argumentos que se expondrán en los
diferentes tipos de párrafos textuales:
- Introducción
- Desarrollo del tema
- Transición
- Conclusión

En los
párrafos de introducción, se advierte cuál es la idea que se va a tratar en
todo el texto, es decir, se aporta un breve adelanto del tema.
Los
párrafos que desarrollan el tema, se refieren a aquellos que detallan, explican
y ejemplifican los diferentes aspectos que se abordan a lo largo del texto.
Por otra
parte, los párrafos de transición, funciona a manera de conector o puente, ya
que se recurre a ello cuando se desea realizar algún cambio de idea, es decir,
cambiar o pasar de un subtema a otro, y pueden usarse también, para adelantar
lo que sigue.
El último
tipo de párrafo el de la conclusión, es aquel que siempre irá en la parte final
del ensayo, ya que su función es darle un desenlace lógico al texto. Se trata
de un resumen de lo expuesto a lo largo de la exposición, y para ello, hay dos
maneras de construirlo; la primera es básicamente un resumen de lo expuesto,
por lo que se recapitulan las ideas antes desarrolladas. La segunda, en cambio,
es una forma de ir “hilvanando” en los últimos párrafos las ideas expuestas
para derivarlas en la conclusión, de tal manera que ya no habrá necesidad de
hacer un resumen.
En un
ensayo desarrollas tu punto de vista sobre un tema, y para escribirlo es
recomendable plantearte los siguientes pasos:
- Introducción
- Desarrollo del tema
- Transición
- Conclusión
En los
ensayos, al tratarse de textos donde se exponen hipótesis, posturas, argumentos
u opiniones, es probable que identifiques, además, párrafos donde:
- Expreses situaciones en las
que se presentan dificultades para el logro de algo.
- Decir que debe suceder u
ocurrir algo ante una determinada situación.
- Explicar razones o causas para
que algo suceda.
Para
integrar descripciones localizadas en diversas fuentes, puedes hacerlo a través
de citas textuales, o bien valiéndote de la paráfrasis. Asimismo, toma en
cuenta que para redactar de manera clara y lógica un texto, debes identificar
previamente las ideas principales.
Lee el
siguiente ejemplo para que quede más claro.
Por último, toma en cuenta que, en la redacción de un texto argumentativo, es de utilidad la inserción de ejemplos, los cuales te pueden servir para argumentar, ilustrar, explicar o demostrar lo que estás exponiendo en tu ensayo. Su función es dar claridad y comprensión, así que recuerda revisar si en el caso de tu texto es pertinente incorporar algunos ejemplos para aclarar las ideas que ahí se exponen.
¿Qué
hacemos?
Al escribir
un ensayo, y con el fin de facilitar la comprensión del lector, quien elabora
un texto argumentativo debe tomar en cuenta que, en cada párrafo del documento,
deben estar desarrolladas de manera lógica las ideas.
Para que un
párrafo esté bien estructurado y tenga coherencia, debe estar vinculado con el
resto de los párrafos sin que se pierda de vista cuál es el tema central que se
está tratando en cada uno.
En el caso
de los textos informativos, como el ensayo que has estado elaborando, es muy
importante cuidar no solo que la información sea objetiva y veraz, sino
también, que las secuencias o el orden de las ideas y el contenido en general,
estén desarrollados de manera coherente.
Recuerda
que la veracidad de un texto está relacionada no solo con el tipo de
información y datos que se proporcionan, sino también con las fuentes y la
forma de utilizarlas.
También se
cuenta con herramientas prácticas de apoyo gráfico como son: Las tablas,
gráficas y las lustraciones en los textos informativos, con el que observas
ahora, su fin es organizar y resumir ideas y conceptos de manera visual. Estos,
permiten la interpretación de forma rápida y fácil.
Puedes usar tablas, gráficos, ilustraciones.
 Observa cómo te puede ayudar cada
uno de ellos.
Observa cómo te puede ayudar cada
uno de ellos.

Toma en
cuenta que ningún texto que se escriba queda bien “a la primera”, por eso es
recomendable hacer una primera versión, es decir, un borrador, y que esa
primera versión, se revise, analice y corrija con paciencia y autocrítica hasta
que tenga una buena forma, ¿Cómo puedes saber cuándo está listo? es necesario
leerlo varias veces hasta identificar los aspectos que se puedan mejorar o
corregir.
Para
revisar la redacción de tu ensayo, sugiero que identifiques las comas; los
puntos y seguido, así como las marcas de género, número y persona, no olvides
verificar la concordancia de las oraciones.
Es
importante consultar diccionarios o manuales de redacción. Recuerda que saber
utilizar los signos de puntuación permite la redacción correcta de los
documentos.
Los
aspectos gramaticales se aprenden con el uso, por eso recomiendo escribir las
veces que sea necesario y leerlo en voz alta, de esta manera, te darás cuenta
de que tu redacción fluye adecuadamente y te podrás dar cuenta cuando tu texto
está bien escrito, y sobre todo de la precisión y claridad de las ideas a
comunicar.
Es bueno
tener la libertad de equivocarse en el borrador, pero una vez que ya estamos
seguros, continua con la integración de la información que investigaste.
Una buena
técnica es con base a lo que has leído es ir incorporando tu opinión, ya que te
has documentado lo suficiente, y también puedes redactar tu ensayo haciendo uso
de paráfrasis.
La versión
final de tu ensayo debe pasar por un proceso de edición, es decir, de selección
de material, que quede justo lo que necesitas.
El proceso
de edición es importante, por ello será conveniente que consideres en la medida
de lo posible, las siguientes sugerencias:
- Establecer de manera uniforme
los márgenes, es decir, el espacio destinado para el texto.
- Numerar las páginas.
- Seleccionar los espacios donde
se insertarán los apoyos gráficos: Tablas, diagramas, esquemas e
ilustraciones, entre otros.
- Escribir con letra legible, si
se hace a mano, o bien con apoyo de un procesador de textos.
- Resaltar los títulos o
subtítulos de los temas y subtemas que se traten.
Es
fundamental que en este tipo de textos se incluyan todas las referencias de
textos consultados. Para ello, revisa y verifica los datos de las fichas
bibliográficas que hayas elaborado cuando llevaste a cabo la etapa inicial de
búsqueda y selección de textos para delimitar el tema.
Hacer un
ensayo necesita tiempo y dedicación así que ¿Cómo elegir de qué tema vas a
escribir? ¿De qué quieres investigar?
Sabes que
lo principal es elegir el tema y delimitarlo, lo que da respuesta a la pregunta
¿Qué quiero investigar? Además, recuerda que entre las características
principales que debiste tomar en cuenta al redactar tu ensayo, es la
argumentación, la cual consiste en dar a conocer las razones que corroborar
nuestro punto de vista. En este sentido, es necesario que los argumentos usados
al redactar un texto, se formulen a partir de la información obtenida en las
fuentes consultadas.
Te
recomendamos que busques en tu libro de texto el aprendizaje esperado: “Argumentar
sus puntos de vista respecto al tema que desarrolla en un Ensayo y lo sustenta
con información de fuentes consultadas” con el fin de reforzar tu
aprendizaje de la sesión de hoy.
El Reto de
Hoy:
Te propongo
un reto para que en los próximos días lo lleves cabo.
Piensa en
una situación real de tu familia o de tu calle o colonia en la que te gustaría
que todos participaran.
- Escribe los principales
aspectos, por los que te interesa dicha situación.
- Piensa cómo convencerías a
participar a los integrantes de tu familia o las personas que viven en tu
calle o colonia.
- Busca información que respalde
tus argumentos.
- Escribe un texto
argumentativo, breve, y compártelo con tu familia.
CIENCIAS QUÍMICA
¿Cómo medimos las propiedades intensivas de los materiales?
Aprendizaje
esperado: Identifica las propiedades extensivas (masa y
volumen) e intensivas (temperatura de fusión y de ebullición, viscosidad,
densidad, solubilidad) de algunos materiales. Explica la importancia de los
instrumentos de medición y observación como herramientas que amplían la
capacidad de percepción de nuestros sentidos.
Énfasis: Medir
algunas propiedades intensivas de los materiales.
¿Qué vamos
a aprender?
Recuerda
que una de las limitaciones al tratar de medir la materia mediante
nuestros sentidos es que los datos obtenidos no son confiables ya que
dependen de la capacidad de percepción de las personas.
¿Qué
instrumentos utilizamos para medir las propiedades intensivas de la materia?
El propósito de esta sesión es medir las propiedades intensivas de algunas sustancias de uso cotidiano, a través de la experimentación.
Escribe en
tu cuaderno el reporte de práctica de los experimentos que se desarrollaran a
continuación tu reporte debe contener los siguientes datos, observa:

Finalmente
reflexionarás sobre lo aprendido respondiendo las siguientes preguntas:

Las dudas,
inquietudes o dificultades que surjan al resolver los planteamientos los puedes
disipar consultando tu libro de texto de Ciencias. Química en el tema 2 del
bloque 1.
Los materiales que vas a utilizar en esta sesión y con los que cuentas en casa son los siguientes:
- 270 ml de aceite comestible de
reúso
- 2 ml de miel
- 22 ml de detergente líquido
- 2 ml de alcohol
- 590 ml de agua
- 120 g de sal
- 3 vasos transparentes
graduados en centímetros
- 2 vasos transparentes del
mismo tamaño
- 3 piedras de un gramo cada una
o canicas de la misma medida
- Botella trasparente
- Cronometro o un reloj
- Cinta adhesiva
- Regla
- Bolígrafo
- Bitácora científica
- Tu libro de texto de Ciencias.
Química.
- Recipiente plástico con tapa
de 1L para tratamiento de desechos.

Es
importante que no repitas experimentos donde se utiliza fuego o termómetro, ya
que los materiales que se usan en un laboratorio están especialmente diseñados
para soportar altas temperaturas de ebullición y fusión, los vasos y
termómetros clínicos que tenemos en casa no cumplen con esas características,
si se utilizan por error pueden provocar accidentes.
Identifica
siempre las sustancias con las que estás trabajando, etiquetándolas con su
nombre.

Investiga
acerca de su adecuado uso y manejo y si es necesario coloca un pictograma que
te permita tomar las medidas de seguridad pertinentes.
Sabías que
1 mililitro (ml) de aceite de cocina que se arroja al agua, contamina 1000
Litros (L).
Conocerás
cómo se pueden medir algunas propiedades intensivas de la materia y te darás
cuenta de que están presentes en nuestra vida cotidiana.
Reflexiona
sobre cómo aplicar este conocimiento a tu contexto inmediato. Analiza la
siguiente presentación:

Para
extraer la sal de la salinera se canaliza el agua del océano en balsas planas
de poca profundidad, esperan a que la luz solar evapore el agua, y el viento
cristalice la sal de cloruro de sodio mezclada con otras sales.
La obtención del cloruro de sodio conocido como sal de mesa, implica separarlo de las otras sustancias, aprovechando las propiedades que la diferencian del resto.
¿Sabías
qué? Por cada 1000 ml de agua hay 35 gramos de sales disueltas y que de estos
35 gramos el 80% corresponde al cloruro de sodio, también conocido como sal de
mesa.

Según el
proyecto de Norma Oficial Mexicana-SAGARPA 2018, la sal de mar debe cumplir con
las siguientes características sensoriales: Ser una sustancia formada por
cristales blancos, inodora de sabor salino franco, soluble en agua y con un
grado de pureza de 99.90%, para el consumo humano.
Con el fin
de comprender este fenómeno y proceso natural desde una perspectiva científica,
realiza si es posible, el siguiente experimento parecido a lo que sucede en las
salineras. Comienza por simular el agua del océano formando una
disolución de 100 ml de agua mezclada con 5 gramos de sal.
Posteriormente
vacía la disolución en un contenedor, sobre el cual pondrás un tapón de corcho
e introducirás un termómetro para medir la temperatura exacta a la que
comenzará a hervir el agua.

100 ml de agua, matraz, 5 gramos de sal,
estufa, termómetro, tapón de corcho.
|
¿Por qué
es importante medir las propiedades intensivas? |
¿Qué
propiedades se aprovechan en el funcionamiento de un instrumento adecuado para
medir la temperatura de ebullición, la temperatura de fusión, viscosidad,
densidad y solubilidad?
Las
propiedades intensivas, como la dilatación y contracción térmica son dos
propiedades que se han aprovechado para construir instrumentos de medición,
llamados termómetros.
Los
termómetros se clasifican de acuerdo con su uso:
- Clínicos: Tienen un rango de
medición de temperatura de 35 a 40 grados Celsius.
- Ambientales: Consideran un
rango de menos 30 a 50 grados Celsius.
- Laboratorio: Miden un rango de
menos 20 a 400 grados Celsius, su funcionamiento se basa en la dilatación
y la contracción térmica las cuales son directamente proporcionales, pues
se encuentran calibrados al incremento o disminución de la temperatura.
En México
los termómetros tienen una escala graduada en grados Celsius, en esta escala
0°C es la temperatura a la cual se congela el agua y 100°C es la temperatura a
la cual hierve, cuando se encuentra a nivel del mar.
Los equipos
que se utilizan a nivel industrial para medir el punto de fusión se basan en el
cambio del estado sólido al estado líquido, registrando la temperatura a la que
sucede dicho cambio.
Estos
equipos utilizan un termómetro unido a la base de un platillo de metal, sobre
la cual se coloca la muestra a analizar y sobre ésta un lente de aumento, que
permite fácilmente observar el cambio de estado, y el registro de la
temperatura.
¿Qué
hacemos?
Es momento
de iniciar con los experimentos, recuerda hacer el registro de tu reporte de
práctica.
Con este
experimento demostrarás que la viscosidad es la resistencia de un líquido a
fluir.
Necesitarás
tres recipientes transparentes con tapa del mismo tamaño, graduados centímetro
a centímetro desde la base hasta la superficie. Colocarás una piedra o una
canica de la misma masa en cada uno de los contenedores. Etiqueta los
recipientes con los nombres de las sustancias que van a contener, e introduce
en cada uno la sustancia con la que fue etiquetado, hasta su total capacidad.
1. Aceite comestible de reúso.
2.
Detergente líquido.
3. Agua.
4. Base
para soportar los recipientes con tapa.
Colocamos
una cinta adhesiva por encima de los recipientes con tapa y antes de voltear
nuestros recipientes. Reflexiona:

¿En qué
recipiente crees que llegará la piedra al fondo más rápidamente?
Registra
tus resultados en una tabla como la que se muestra a continuación.

En este
caso el detergente es la sustancia más viscosa porque la canica tardó más
tiempo en llegar al fondo del recipiente.
¿Tus
resultados confirman o rechazan la hipótesis?

A nivel
industrial para obtener medidas exactas de viscosidad se utiliza un
viscosímetro en el que se manejan unidades de medida como el metro
cuadrado por segundo (m2 /s) y pascal por segundo (Pa·s).
Ambas
consideradas dentro del Sistema Internacional de unidades (SI). Aunque medir es
un acto que realizas con frecuencia en la vida cotidiana, pocas veces reconoces
su importancia durante la experimentación, por lo que cabe destacar que, en el
campo de la ciencia, es gracias a ésta, que has podido conocer y describir las
propiedades de la materia con base en sus diferencias.
Expresar y
graficar los resultados experimentales durante el trabajo científico implica
aislar, reproducir el fenómeno de estudio bajo condiciones controladas y es
este proceso el que nos permite recabar datos valiosos para ser analizados,
interpretados y poner a prueba las hipótesis planteadas.
Cabe
destacar que, en el mundo de la ciencia, no está permitido plantear una
hipótesis sin antes haber realizado una investigación bibliográfica sobre el
fenómeno a investigar.
No
obstante, te sugerimos que te atrevas a plantear predicciones de lo que va a
suceder durante cada experimento y que registres tus hipótesis, a fin de que si
te equivocas te motives a investigar el porqué.
Recuerda
que el conocimiento científico tiene un carácter tentativo, es decir, que nada
es definitivo, pues este avanza al mismo ritmo que progresa la tecnología y la
sociedad. Y recuerda, si quieres aprender en la ciencia química tienes que
experimentar.
Sabías que
un litro de aceite no tiene la misma masa que un litro de agua. Esto se debe a
la propiedad intensiva conocida como densidad, la cual se define como la
relación entre la cantidad de masa en una sustancia por unidad del volumen que
ocupa.

Antes de
medir la densidad de un líquido es importante calibrar el densímetro
colocándolo dentro de una sustancia con un valor bien conocido por el
experimentador, la cual se compara con una tabla de valores también conocidos y
tomados bajo las mismas condiciones de presión y temperatura de la muestra
sobre la que mediremos la densidad.
La densidad
de una sustancia se mide utilizando una probeta que se llena hasta la marca
máxima de su graduación en este caso 250 ml de agua en la primera probeta y
250ml de aceite en la segunda probeta.

Recuerda que para medir adecuadamente el volumen de un líquido utilizando instrumentos volumétricos como lo es la probeta, es importante tomar en cuenta la formación del menisco, el cual puede ser una superficie cóncava o convexa, según si las moléculas del líquido se atraen o se repelen con el vidrio.
La
concavidad del menisco se origina cuando las fuerzas de adhesión entre un
líquido y las paredes del recipiente que las contiene son mayores que las de
fuerzas de adhesión del líquido.
La
convexidad del menisco se da cuando las fuerzas de cohesión del líquido son
mayores que las de adhesión.
La
superficie de los líquidos presenta una propiedad intensiva conocida como
tensión superficial. La cual actúa succionando el líquido cuando el menisco es
cóncavo y rechazándolo cuando es convexo, cualquier material que ingrese al
líquido debe vencer esa fuerza o tensión.
Para
realizar la lectura del líquido en la probeta esta debe estar colocada en una
superficie plana y al medirla debe coincidir la curva que se forma en el
líquido en la parte central con el aforo o graduación de la probeta.
Una vez que
tenemos la medida correcta del volumen mediremos la densidad, para lo cual se
introduce el densímetro verticalmente con cuidado dentro del líquido y
esperamos hasta que flote libre y verticalmente.
Posteriormente
se observa en la escala graduada su nivel de hundimiento en el líquido; esa es
la lectura de la medida de densidad relativa del líquido. La densidad de ambas
sustancias se muestra así:
Para el
aceite 0.84g/cm3 y para el agua 1g/cm3.
Al comparar
el valor de densidad de ambas sustancias puedes comprender que por sus
diferencias de densidad estos dos líquidos son inmiscibles entre sí y puedes
decir que la posición que adoptan cuando ambos se juntan, se le conoce como
densidad relativa.
Observa el
siguiente ejemplo:
Necesitarás
una botella transparente con una cinta adhesiva dividida en tres partes
iguales, pegada en la parte de atrás.
Utilizarás
las siguientes sustancias: alcohol, miel y aceite.
¿Te
atreverías a predecir de manera ascendente la densidad de las sustancias?
Te
sugerimos utilizar la siguiente tabla.

Registra tu
hipótesis en el reporte de práctica. Colocarás las sustancias en la botella,
vertiéndolas en el orden de mayor a menor densidad.
La densidad
de una sustancia varia con la temperatura y también si se disuelve en ella otra
sustancia, de ahí que el orden en el que las viertas en la botella es
importante para mantenerlas separadas.
Es sorprendente como estas sustancias no se mezclan, la densidad sin duda es una propiedad que se puede aprovechar para separar las sustancias de una mezcla. ¿Sabes qué tipo de mezcla es la torre de fluidos?
Para medir
la solubilidad de las sustancias se utilizan curvas de solubilidad, las cuales
son representaciones de la solubilidad de una sustancia en función de la
temperatura.

Observa que
de acuerdo con el plano cartesiano en el eje de las “X se encuentra la
temperatura y en el eje de las “Y” se encuentra el coeficiente de solubilidad
expresado en g de soluto disueltos en 100g de agua.
Resuelve las siguientes actividades en tu libreta utilizando la gráfica de solubilidad de algunas sales en agua, en función de la temperatura.
Puedes
observar que en ella se presentan tres curvas de sustancias distintas cada una.
Identifica la curva que corresponde al soluto con el que vas a trabajar y
guíate sobre esa curva para analizar los datos y encontrar la respuesta
correcta.
El soluto
es cloruro de sodio cuya fórmula química se escribe NaCl.

Para
resolver el primer planteamiento considera que el dato que proporcionan
corresponde al eje de las “X” por lo que te ubicarás en este eje hasta
encontrar 50°C y subirás verticalmente hasta topar con la curva y lee en el eje
de las “Y” que la concentración del cloruro de sodio a 50°C es de 39 gramos de
soluto disueltos en 100g de agua.
2. ¿A qué
temperatura se disuelve el cloruro de sodio si se disuelven 40g de cloruro de
sodio en 100g de agua?
Para
resolver el segundo planteamiento considera que el dato que se proporciona
ahora corresponde a la concentración de la solución que es de 40g de soluto
disuelto en 100 g de disolvente, por lo que nos ubica en el eje de las “Y”
hasta encontrar los 40 gramos y posteriormente caminas en el eje de las “X”
hasta topar con la curva y bajar en el eje de las “Y” para encontrar la
temperatura, la cual corresponde a 90°C.
Establece
que la solución que preparas tendrá una temperatura de 90°C y que la cantidad
del disolvente o agua será de 100g, como te has dado cuenta ya solo modificarás
la cantidad del soluto cloruro de sodio, en el primer caso utilizarás 20 g de
sal, en el segundo 40 g y en el tercer caso 60 g.
Ahora
ubícate entonces en el eje de las “X” dado que la temperatura y la cantidad de
disolvente no cambian y subes verticalmente sobre el eje de la “Y” para
encontrar y marcar cuando llegues a 20g de soluto y colocamos una marca,
posteriormente cuando lleguemos a 40g de soluto y luego a 60g.
Una vez que
has marcado te das cuenta de que la marca que se encuentra sobre la curva
corresponde a la solución saturada, la marca que se encuentra por debajo de la
curva es la correspondiente a la solución diluida y la que se encuentra por
encima de la curva es la solución sobresaturada.

Caracterizar
e identificar las sustancias, es una actividad que se utiliza para la
construcción del conocimiento científico el cual se basa en un conjunto de
procedimientos en los que utilizamos nuestros sentidos para experimentar con
algunos hechos que han despertado nuestro interés.
La
experimentación que llevas a cabo partió del hecho de demostrar cómo es que los
instrumentos de medición amplían la capacidad de percepción de nuestros
sentidos y es que a partir de estos has podido identificar y medir las
propiedades intensivas, temperatura de fusión y de ebullición, viscosidad,
densidad, solubilidad, todas ellas independientes de la cantidad de materia.
El Reto de
Hoy:
Ahora que
has aprendido a medir las propiedades intensivas de la materia puedes concluir
que efectivamente estas no dependen de la cantidad de materia y que su medición
nos ayuda a identificarlas, pues un material puede tener cualquier magnitud de
masa y volumen, pero sólo una y específica magnitud de densidad, viscosidad,
solubilidad, temperatura de ebullición y de fusión.
Los
instrumentos de medición son herramientas útiles y efectivas para poder
cuantificar las propiedades de los materiales, recordemos que para cada
propiedad se emplea un instrumento de medición específico, con excepción de las
temperaturas de fusión y ebullición, estas se miden con el termómetro de
laboratorio.
Entre otras
propiedades observaste que la viscosidad de un líquido es su resistencia para
fluir y en el Sistema Internacional de Unidades se expresa en pascal por
segundo, se mide con el instrumento llamado viscosímetro.
Recuerda es
conveniente sistematizar los resultados obtenidos al experimentar, así como
seguir las normas de seguridad para evitar accidentes.
FORMACIÓN CÍVICA Y ÉTICA
Juntos hacemos el cambio
Aprendizaje
esperado: Propone acciones colectivas para enfrentar
problemas de orden social y ambiental que afectan a la comunidad, al país y la
humanidad.
Énfasis: Recursos
y condiciones para crecer, aprender y desarrollarse en el entorno.
¿Qué vamos
a prender?
Reflexionarás
sobre la importancia de involucrarse y proponer acciones
comunitarias para crecer, aprender y desarrollarse en el entorno, mediante un
análisis rápido de las necesidades y problemáticas que identificas en tu
comunidad.
¿Alguna vez
te has preguntado qué puedes hacer para mejorar nuestra comunidad?
Reflexionarás sobre algunas acciones para lograrlo. Para introducirlos al tema,
es importante que identifiques los indicadores con los que se mide la
pobreza en nuestro país.
Para ello,
conocerás a ver cuál es el procedimiento que utiliza el Consejo
Nacional de Evaluación de la Política de Desarrollo Social, también
llamado CONEVAL, para medirla.
CONEVAL es
la instancia en México que establece los lineamientos y criterios para medir la
pobreza. Esta medición la realiza cada 2 años a nivel nacional y estatal,
y cada 5 años a nivel municipal, a través de la Encuesta Nacional
de los Ingresos y Gastos de los Hogares.
Los 9
indicadores que sirven para medir la pobreza en México son:
- Ingreso.
- Rezago educativo.
- Acceso a servicios de salud.
- Acceso a la seguridad social.
- Acceso a la alimentación
nutritiva y de calidad.
- Calidad y espacios de la
vivienda.
- Acceso a servicios básicos en
la vivienda (agua, drenaje, luz).
- Grado de cohesión social.
- Acceso a carretera pavimentada.
Pero, ¿Para
qué nos sirve conocer estos indicadores?
Entender
los datos que te dan estos indicadores te ayudará a comprender diversas problemáticas de
orden social derivadas de la pobreza y el deterioro ambiental que puede o no
generarse a partir de ellas.
Por
ejemplo, el indicador “rezago educativo” se mide cuando una persona no tiene
escolaridad o que tiene 15 años y no ha terminado la secundaria.
Observa la
siguiente situación. ¿cómo se relaciona con el indicador Rezago educativo y qué
problemáticas pueden originarse de esto.

“Las
mujeres aún presentan niveles de rezago educativo más altos que los hombres,
sobre todo si están en condición de pobreza, sin embargo, es notable la
reducción de esta brecha entre grupos de población de 14 a 44 años”.
“Ana y
Teresa estudian el tercer grado de secundaria. El sueño de Ana es estudiar
medicina; Tere quiere ser bióloga”.
Al escuchar
la primera afirmación, donde se señala que el rezago educativo es más alto en
las mujeres da tristeza, porque a pesar de todas las acciones que se han
llevado a cabo en favor de las mujeres, todavía hay indicadores que muestran
desigualdad.
Pero, por
otro lado, nos da esperanza que, en el grupo de la población de tercero de
secundaria, esta brecha se ha visto disminuida.
Pero
¿Cuáles serían las problemáticas que pudieran derivarse para Ana y Tere?
Si viven en
situación de pobreza, hay posibilidades de que no cumplan sus sueños, que Ana
no estudie medicina y Tere no llegue a ser bióloga. Pero también hay que
considerar que el rezago educativo no sólo no les permitiría cumplir con sus
sueños, sino que podría llevarlas a una serie de obstáculos para su desarrollo
integral y que en un futuro no puedan mejorar su calidad de vida.
Además, las
problemáticas derivadas por el rezago educativo no sólo afectan a quienes no
pueden continuar con sus estudios, sino a todos los habitantes del país, porque
entre más bajo sea este indicador, se verá reflejado en el crecimiento y
desarrollo del país en todos los sentidos. Al mejorar el indicador la economía
mejoraría, habría más fuentes de empleo, se daría apertura a la innovación en
las diferentes áreas y la calidad de vida de las personas se vería beneficiada.
Entonces,
además de conocer los indicadores, todos debemos colaborar para que cada vez
sean menores, ya que la pobreza no sólo afecta a una persona o grupo, sino a
todo el país.
Los
indicadores nos ayudan a direccionar las acciones que necesitas emprender desde
tu hogar, escuela y comunidad para poder generar cambios positivos para todos.
Es un buen
momento para reflexionar y tomar notas para responder la siguiente pregunta:
¿Qué
problemas identificas en tu comunidad que estén relacionados con los
9 indicadores que miden la pobreza?
Considera
cuáles son los que se necesitan resolver más urgentemente. Eso no sólo es
tarea de una persona, sino de toda la comunidad.
Lee la
siguiente frase del filósofo y ensayista español, José Ortega y Gasset. Piensa
de qué forma se relaciona con nuestro tema.

Esta
reflexión que hizo José Ortega y Gasset te lleva a pensar sobre tus acciones.
La base de ellas es el esfuerzo, que no sólo es un esfuerzo individual, sino
colectivo.
Anota en tu
cuaderno si recuerdas alguna o algunas experiencias de trabajo colaborativo.
Piensa en cómo fueron y si lograron cumplir la meta.
Durante el
proceso, seguramente te enfrentaste a diversas situaciones que te llevaron a
reconocer tus fortalezas y tus áreas de oportunidad.
Recuerda
que el Trabajo Colaborativo es muy importante para el
mejoramiento del entorno en el que vives, ya que permite que todos participen
aportando lo que puedas y sepas hacer mejor.
Al final,
como dice la frase que acabas de leer, te construyes y te fortaleces como ser
humano, trabajas en conjunto, independientemente de los resultados.
Lee con
atención el siguiente caso y anota en tu cuaderno las respuestas:
En un
concurso de cocina 2 equipos de 5 integrantes cada uno, llegaron a la final.
Para poder ganar necesitaban realizar un banquete para 50 personas que
incluyera la entrada, la pasta, el plato principal y el postre. Para ello se
organizaron de la siguiente manera:
En el
equipo 1, Pedro, que es experto en realizar pasteles y dulces típicos
mexicanos, se autonombró el “organizador del equipo” y asignó a sus demás
compañeros la realización de la crema para la entrada, el espagueti y de plato
fuerte mariscos, encargándose él del postre y de supervisar el trabajo de sus
compañeros.
Sin
embargo, se le olvidó preguntar a sus compañeros si sabían realizar los
platillos asignados o si alguno era alérgico a algún alimento.
Desafortunadamente,
uno de los integrantes del equipo, a quién se le asignó realizar el plato
fuerte, era alérgico a los camarones, por lo que nunca probó el platillo.
También sucedió que a quien le tocó hacer el espagueti, era experto en carnes
rojas y le quedó crudo. Cuando pasaron a evaluar el banquete, el equipo perdió
porque le hacía falta sabor al platillo principal y la pasta estaba mal cocida.
El equipo no tuvo muy buenos resultados.
Ahora,
analiza al equipo 2 quienes comenzaron reuniéndose para ponerse de acuerdo.
Antonio
expuso a los integrantes que tenía experiencia en la preparación de pastas y
asumió esa responsabilidad.
Luis, otro
integrante comentó que tomó un curso de repostería por lo cual se sintió
preparado para realizar el postre.

Lolita, que
no tenía experiencia en postres, se ofreció a apoyar a Luis en su elaboración.
Enrique y Tamara se pusieron de acuerdo para realizar la crema y el plato fuerte. Los 5 terminaron sus platillos a tiempo y ganaron el concurso.

Ahora,
escribe en tu cuaderno las respuestas a las siguientes preguntas.
- ¿Qué factores
facilitaron el trabajo del Equipo 2?
- ¿Qué factores dificultaron
el trabajo del Equipo 1?
- ¿Qué equipo trabajó de forma
colaborativa?
Es
importante que sepas distinguir entre el trabajo en equipo y el trabajo
colaborativo.
La
diferencia tiene que ver básicamente con los fines y los medios.
En un
trabajo en equipo lo que importa es el fin, es decir, el objetivo o la meta
planteada, mientras que en el trabajo colaborativo lo más importante es el
medio o el proceso mediante el cual se llega al fin o a la meta, es decir, el
“Cómo se trabaja”.
En el
equipo 1, que realizó trabajo en equipo, alguien asumió el liderazgo,
repartiendo los roles y tomando las decisiones importantes.
Aun cuando
cada integrante pudo haber sido muy bueno, no tuvieron oportunidad de expresar
su voz y su creatividad.
Mientras
tanto, en el equipo 2, que realizó trabajo colaborativo, cada integrante eligió
libremente la responsabilidad que quería asumir.
Como verás,
esta es una de las claves de la democracia. Bajo este principio, desde hace
algunas décadas, la ciudadanía se ha organizado para contribuir con las
autoridades en la solución de problemas o necesidades que afectan a las
comunidades.
Analiza cómo, desde
el trabajo colaborativo y el interés personal, puedes intervenir en nuestra
comunidad para enfrentar los problemas o atender las necesidades que identificaste anteriormente.
Para
ello analizarás qué se entiende por ciudadanía democrática organizada y de
qué forma puedes participar.
¿Qué
hacemos?
Observa el
siguiente video:
- Ciudadanía democrática organizada.
Aprende en
Casa https://www.youtube.com/watch?v=oPlkjoROVp4
¿Sabías que
en México hay 42,269 organizaciones ciudadanas, mejor conocidas como
Organizaciones de la Sociedad civil o OSC?
Son
organizaciones de ciudadanos que trabajan para hacer visibles los problemas que
afectan a las comunidades ante las autoridades.
Pero, ¿Para
qué necesitan a los demás y para qué crees que los demás los necesitan?
Esas
preguntas son esenciales, porque es lo primero que se debe definir cuando
quieres colaborar y participar por el bien de nuestra comunidad, nuestro país y
la humanidad. Es decir, ¿Cuál es el problema que se necesita resolver? y ¿De
qué se trata?
Para ello
puedes recurrir a los 9 indicadores que sirven para medir la pobreza en México
y que analizamos al inicio.
Repasa
cuáles son:
- Ingreso.
- Rezago educativo.
- Acceso a servicios de salud.
- Acceso a la seguridad social.
- Acceso a la alimentación
nutritiva y de calidad.
- Calidad y espacios de la
vivienda.
- Acceso a servicios básicos en
la vivienda (agua, drenaje, luz).
- Grado de cohesión social.
- Acceso a carretera
pavimentada.
Una vez que
se tiene detectado el problema o necesidad que se quiere atender, es preciso
que te preguntes:
- ¿Cómo afecta a las personas
ese problema?
- ¿Qué es necesario para
resolverlo?
- ¿A quién puedes acudir para
que se solucione?
- ¿Qué beneficios tendría para
la comunidad que se atendiera la situación?
Escribe una
propuesta para resolver alguno de los problemas o necesidades que
identificaste. Señala los indicadores con los que
se relacionan y describe el impacto que tendría en su comunidad la
participación de todos en la solución del mismo.
No olvides tomar
en cuenta que tus vecinos, amigos, familiares y compañeros de escuela podrían
colaborar.
El Reto de
Hoy:
En esta
sesión identificaste los problemas y necesidades sociales de tu comunidad,
y retomaste el trabajo colaborativo como base para proponer acciones que
mejoren el entorno en donde vives, identificando las ventajas de llevarlo a
cabo y las personas que podrían ayudarte a realizarlo.
Recuerda la
frase de Ortega y Gasset: sólo se aguanta una civilización, si muchos
aportan su colaboración al esfuerzo.
TECNOLOGÍA
Información no disponible
______________________________________________________
Disponible en PDF https://1drv.ms/b/s!AtyXssd0mRTWkpEGFfu2pGuwEbX6PQ?e=tWd9Mc

























No hay comentarios:
Publicar un comentario